


Next: Implications of Theorem 3
Up: Theorem 3
Previous: Theorem 3
This is tricky, but a TM M accepting an r.e. language will always
halt for 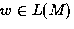 . Since w is always in either L or
. Since w is always in either L or 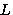 ,either M or
,either M or 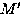 will always halt. But, by Theorem 1, the
complement of a recursive language is recursive. Therefor, both L
and
will always halt. But, by Theorem 1, the
complement of a recursive language is recursive. Therefor, both L
and 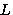 are recursive if both are r.e.
are recursive if both are r.e.
root
6/10/1998