Non-deterministic FAs

A non-deterministic FA is an FA with more than one mapping for a single state-input pair.

An example of a non-deterministic FA is presented which accepts strings with either two consecutive zeros or two consecutive ones.

Question as to which transition to make in response to input. Automata forks to produce parallel automata parsing input. Input is accepted if any parallel automata accepts. Otherwise reject.

This following table describes the non-deterministic FA:

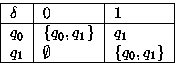$$\centerline{ \begin{tabular} {\vert l\vert l\vert l\vert} \... ...tyset $\space & $\{q_0, q_1\}$\space \\ \hline \end{tabular}}$$ (1)

These equations and the following table describe the deterministic equivalent:

$$M^{\prime} = ( Q^{\prime}, \{0,1\}, \delta^{\prime}, [q_0], F^{\prime})$$ (2)

$$Q^{\prime} = \{ [q_0],[q_1],[q_0,q_1], \emptyset \}$$ (3)

$$\begin{tabular} {\vert l\vert l\vert l\vert} \hline $\delta... ...[q_0, q_1]$\space & $[q_0,q_1]$\space \\ \hline \end{tabular}$$ (4)