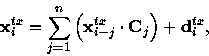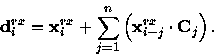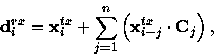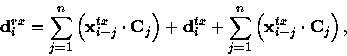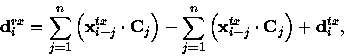


Next: Project Summary
Up: LFSR Signal Spreading
Previous: LFSR Signal Spreading
Note: The algorithm described here comes from the Spring 1998
notes for Neil Gershenfeld's ``Physics of Information Technology''
class, which are soon to be published in book form.
Given a shift register of length n, a tap vector 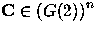 (a
vector of bits of length n), and a data bit
(a
vector of bits of length n), and a data bit 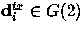 ,the next encoded bit
,the next encoded bit 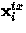 is calculated by
is calculated by
| 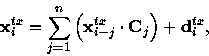 |
(1) |
where addition is define as logical XOR and multiplication as logical
AND. Given a shift register of the same length, an identical tap
vector, and a received bit 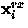 , a data bit
, a data bit
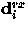 is decoded from the encoded stream as
is decoded from the encoded stream as
| 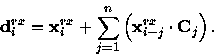 |
(2) |
Assuming 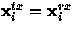 , then
, then
| 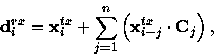 |
(3) |
| 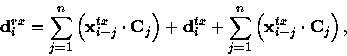 |
(4) |
but since addition and subtraction are equivalent in this basis,
| 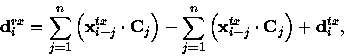 |
(5) |
| 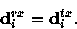 |
(6) |
Thus, if transmission occurs without error, the original signal can
be reconstructed perfectly. Even assuming noisy transmission,
encoding schemes can be used on top of the LFSR spreading to ensure no
data is lost.



Next: Project Summary
Up: LFSR Signal Spreading
Previous: LFSR Signal Spreading
root
5/22/1998
![]() (a
vector of bits of length n), and a data bit
(a
vector of bits of length n), and a data bit ![]() ,the next encoded bit
,the next encoded bit ![]() is calculated by
is calculated by