EyeBox: A Cheap, Effective 3D Scanner for Volumetric Reconstruction and Object Recognition
12.15.02
Simon
Greenwold
Aesthetics + Computation Group
MIT Media Lab
2.20.03 Update: The new system is working. It consists of three webcams, two flourescent lights, a turntable from a microwave, a gutted Apple Cinema display, and a mini-fridge.
|
|
||||
|
[click here to see a movie of Gumby being reconstructed from images] |
|
EyeBox is a component technology in a larger project under development called The Associate, which aims to use physical objects instead of names as referents for digital information. You place an object from your environment into The Associate (a box much like EyeBox). The object is quickly scanned and matched against other objects that have been placed in before. If the object is new, you are prompted to pull on top of it any set of files or information that you want to permanently associate with it. For instance, you may pull a contact list onto your cell phone. Then you may remove the object from the box. Any time you place the object back into the box, all of the files associated with it are pulled up for your perusal. Instead of trying to remember what you called documents, folders, and projects, you created years ago, you can remember them by the objects you associated with them. This is an attempt to provide you with stronger and richer associative cues than file names for your information. You are also free to store and organize digital information using the physical referents. Some things are best tossed into a shoebox. Some things are best displayed on a shelf. The Associate gives you the ability to apply real spatial organization to digital information.
The problem that EyeBox solves is the recognition problem that The Associate poses: How can we quickly recognize any object that you place into the system regardless of its orientation, having seen it perhaps only once before from a different angle? We know that objects look radically different from different viewpoints. We need some invariant property to use for recognition. Options include, color, mass, spatial moments, or volume envelope. EyeBox uses quickly computed spatial properties of the object's volume for recognition.
Another goal in the project was to keep costs low. Very nice 3D laser digitizers are available for $25,000. EyeBox is not as accurate as these, but it cost $100 to build. There is an obvious place for such devices in industries such as rapid fabrication, design, and entertainment.
Precedents

reconstructed ball-kicker from [2]
The technique of reconstructing volume from silhouette data is not new. It is well worked out and documented in a variety of sources. Typical setups for the process involve a single well-calibrated camera viewing an object on a turntable as in Kuzu and Rodehorst [1]. The turntable is turned by hand or motorized to provide an arbitrarily large number of silhouette images to be acquired from a single camera. My setup avoids this procedure in the interest of speed and simplicity. The six webcams in my setup are fixed in their positions. There are no moving parts. The images are acquired not literally simultaneously, but in a matter of seconds, a speed impossible with a turntable. There are only six images, however, not sixty as is common in turntable setups. But I was shocked how well reconstruction can be achieved from so few observations. Of course, the low cost of the system means that it is easily scaled as well. I could double the number of cameras for another $100.
Other fixed camera setups exist, notably Matusik, Buehler, and McMillan's [2], which is capable of scanning people in a room in real time. This setup requires a computer per camera and one more as a central processor, so it doesn't qualify as a low-cost solution, but their results are stunning. It is also not designed for scanning handheld-sized objects. I intend to implement algorithms of theirs for texture mapping the objects' images back onto their 3D forms.
The first step in the construction was the dismemberment of the webcams. Then I built an 18" X 18" X 18" cube out of foam core with a plexiglass shelf in it 7" from the bottom. I cut holes in the sides and top for the cameras and attached two small fluorescent lights to the inside. The third image shows the box with the top off and my calibration object, a 4" X 4" X 4" stick-frame cube with color-coded edges, inside. Calibration of the cameras was a two-step process. The first step was the intrinsic calibration, which I accomplished with the help of the OpenCV computer vision library from Intel. The extrinsic calibration proved to be harder, so I constructed my own software to do it, shown in the fourth image. Looking from the point of view of each camera, I manually adjusted the camera's extrinsic parameters so that the projection of the calibration object matched the image. Then I was ready to write the reconstruction software.
The first step was to acquire a silhouette image from each camera, which was very easy because of the well-controlled imaging environment. For each camera, I simply subtracted an image of the empty box and then thresholded the results.

Images of the same setup as taken from each of the six cameras before
silhouetting.
Techniques for reconstructing form from silhouette data are all capable of producing its "visual hull" relative to the views taken. Abstractly, the visual hull of an object is the best reconstruction that can be made of it assuming views from every angle. The visual hull, as discussed in Petitjean [3], is a subset of an object's convex hull and a superset of its actual envelope. Specifically, it cannot ever recover a full indentation, such as the inside of a bowl. Such an indentation will be filled in by the visual hull.
Methods of visual hull processing fall into three categories: image-based, polyhedral, and volume carving. All of these techniques rely on the same basic principle—that a silhouette relative to a calibrated camera produces a cone of volume in which the object must be located. These cones from several cameras can be intersected to produce a representation of the volume that they are all looking at. It takes surprisingly few cameras to get a fairly good approximation of most shapes.
This is the simplest technique to implement and also the slowest. It projects voxels from world space onto each of the camera views. If a voxel projection falls fully outside any of the silhouettes, it can be discarded. This produces an explicit volumetric representation at the cost of voxel aliasing and lots of computation. I implemented it because I wanted a volumetric representation for matching purposes and it was the easiest to produce. It is also by means of its aliasing somewhat more tolerant of error in camera calibration than the polyhedral method.
Speeding it up
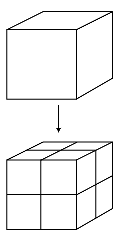
octree subdivision
Having chosen the volume carving method, I sped it up by representing the volume as an octree. That is an iteratively refined volumetric tree starting with a root node representing the entire volume to be scanned. When a projected node is found to be cut by the silhouette from any camera, it is divided into eight subnodes as shown on the left. This way whenever a large node is found to be outside of any of the projections, it need never be subdivided or otherwise considered again. This speeds processing up dramatically. Another speed advance was to iteratively refine the octree representation by one level at a time, running it on each camera at each level. That way more large octree nodes were rejected earlier, and did not slow it down. Octree nodes that were wholly inside each silhouette were marked too, so that on each iteration, the only nodes that had to be processed were nodes that in the previous level intersected silhouette boundaries in some camera. This is tantamount to finding the substantial structures early and then iteratively refining the surface. It also means that you see the form improving over time and you are free to stop the process whenever it gets to a level you are happy with. Smoothing of the surface can then be done with something like marching cubes.




the iterative refinement of Gumby
Camera Placement
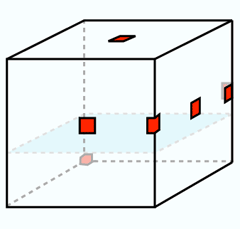
Red squares mark the placement of the six cameras. The blue plate is
the transparent plexiglass surface on which the object sits.
Reconstruction works like a dream. The software shows the empty box image on the left, next the original image taken from the camera, then the differenced image, and finally the thresholded difference. The reconstructed object is rendered in OpenGL, and can be rotated any direction.

Reconstruction of a small flexible camera tripod.
There are some problems with the reconstructed objects. Many of them have to do with the white background. Light colored objects do not work well at all. Specularities on objects are always white and tend to be seen as background, drilling holes in objects. Reflections off the plexiglass are troublesome. In a future version of the system, I would use a blue background to make segmentation simpler. Finally, the box is rather large for an effective scanning volume of 6" X 6" X 6". That could be improved with wider angle lenses, but the wider the field of view, the lower the quality of the reconstruction. There are also errors of volume just due to spaces not visible to any camera. This could be helped with more cameras.
Object recognition
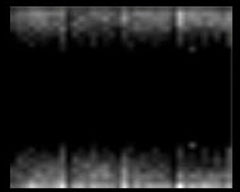
The volume signature of a squash.
Once volumetric reconstruction was accomplished, I turned to object recognition by volume. The problem was to find a similarity metric invariant to translation and rotation on any axis. Initially I tried doing a principal axis transform to align the objects with their major moments. But I found that the principal axis calculation was highly sensitive to small errors. A slightly different reconstruction of the same object could easily have its principal axes switched.
I then decided to give each volume a signature calculated as a rotational volumetric histogram. I iterated over each voxel present in the object's volume and calculated its spherical coordinates relative to the object's centroid. Then I binned the value by its two angles into a 36 X 36 matrix, making a 2D histogram of volume by spherical angle.
I tested the similarity of two volume signatures by comparing them with a Euclidean distance norm. I would, however, iterate, shifting the comparison over by one value at a time to find the least distance for two signatures because if the object was in a different orientation I expected the volume histogram to be arbitrarily translated.
I stored the volume signatures of ten different objects and then tested the recognition with different translations and orientations of the same objects. It got half of them right. The ones it got correctly, it would get right in any orientation or position. Of the ones it got wrong, it misidentified them as the same few objects every time. The consistency gives me hope that the technique can be improved. For one thing, all of the signatures seem to be blank in the middle, which leads me to believe that the spherical coordinates are underrepresenting the bins at the north and south poles. I will try to find a mapping that gives a fuller signature. I should also be using a robust distance metric.

A correct match of a hot glue gun. See the proposed match
on the right above the volume signature.
The recognition portion has a long way to go, but I am optimistic. There are simple invariants such as color to add to the mix, which should help a lot. I am very pleased with the results of the reconstruction, but may move to a polyhedral representation for accuracy and speed. EyeBox clearly demonstrates the feasibility of a low cost 3D scanner and recognizer.
[1] Y.
Kuzu and V. Rodehorst, Volumetric Modeling Using Shape From Silhouette,
www.fpk.tu-berlin.de/forschung/sonder/pub/DT4_kuzu.pdf.
[2] W. Matusik, C. Bueler, and L. McMillan. Polyhedral visual hulls
for real-time rendering. In Proceedings of Twelfth Eurographics Workshop
on Rendering, pages 115-125, June 2001.
[3] S. Petitjean, A Computational Geometric Approach to Visual Hulls,
Int. J. of Comput. Geometry and Appl., vol. 8, no.4, pp. 407-436, 1998
[4] S. Sullivan and J. Ponce, Automatic Model Construction, Pose Estimation,
and Object Recognition from Photographs Using Triangular Splines, IEEE
Transactions on Pattern Analysis and Machine Intelligence, 20(10):1091-1096,
1998.









