6. Overhanging Truss
 |
6. Overhanging Truss |
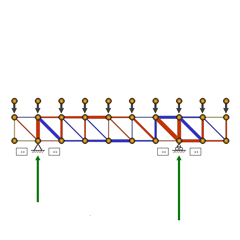
| The Screen | The Form Diagram shows a nine-panel truss
with two supports. Its Force Polygon is to the right, and
numerical member forces are tabulated below.
The Toggle Switches will all be familiar to you by now. But a new feature of this demonstration is seen just inside each reaction: A box with twin arrows in it. Click on this box to see what happens. Notice that another control box appears when you do this. You may move any node that is marked with a yellow circle. All the other parts of the screen will change instantaneously to reflect the consequences of each move–the reactions are recalculated, the force polygon is modified, and the values of member forces change.
|
||||
| Exercise One | Play | ||||
Use the mouse to play with the overhanging truss in any way that you like. Move the supports in and out. Move some of the yellow circles to explore the possibilities and discover how the various features work. Vary the loads. Try the various toggles.
|
|||||
| Further Exercises | Experiment | ||||
Some minimal guidance as you work with this demonstration: |
|||||
| 1. Why are members 9-10 and J-18 zero-force members? 2. Move one support in to create a three-panel overhang. Notice the zero-force segments in the top and bottom chords. What is going on here? 3. Move the supports in and out, and observe how the member forces change
as you do this. Also notice how the Force Polygon changes: |
|||||
a. How are the changing reactions reflected in the load line? b. What accounts for the movement of the Force Polygon back and forth across the load line? c. Move both supports in as far as they can go. Change the shape of the truss to resemble as closely as possible a portion of the famous Firth of Forth Railway Bridge, working from a photograph if at all possible. Examine the Force Polygon that results from this form–what can you say about it? d. Experiment with changing the form of the truss as you try various
support locations, trying to find an efficient form for each condition.
Do the same for some different loading conditions. |
|||||